스택 (Stack)
스택은 후입선출(LIFO : Last In First Out)로 처리되는 자료구조이다. 즉 스택의 가장 마지막에 들어간 요소가 가장 처음으로 꺼내진다.
다시말해 데이터의 삽입과 삭제가 데이터의 한쪽 끝에서만 일어난다.

위와 같은 구조에서 우리는 크게 두가지 행동을 할 수 있다.
- 새로운 접시를 추가하는것.
- 맨 위의 접시를 제거하는것.
만약 새로운 접시를 맨 아래에 놓거나, 맨 위가 아닌 특정 위치에 놓고싶다면 놓고싶은 위치를 기준으로 위에 있는 접시들을 모두 제거한 후 추가해야한다.
이것이 바로 스택이 작동하는 방식이다.
후입선출(LIFO : Last In First Out)의 원리
Stack 위에 어떤 원소를 집어넣는것을 Push 라고 하고, 원소를 제거하는것을 Pop 이라고 한다.
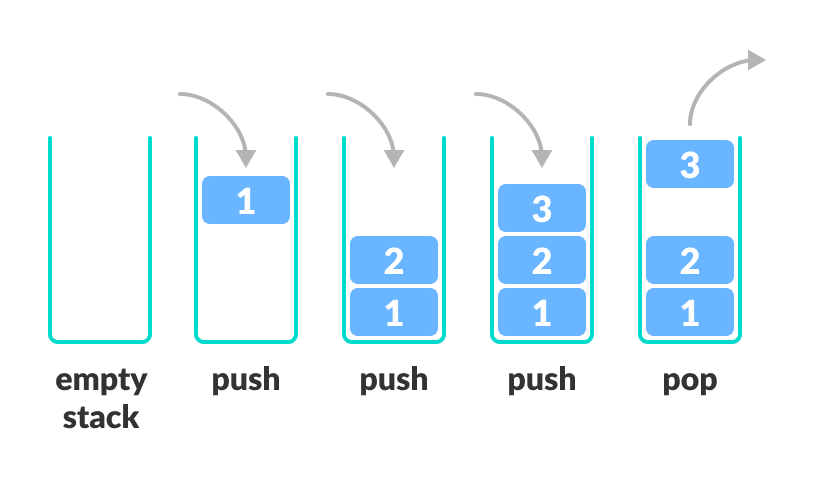
위에서 원소 3은 제일 마지막으로 스택에 추가되었지만, 제거될때 제일 먼저 제거되었다.
이것이 바로 후입선출(LIFO : Last In First Out)의 원리이다.
C, C++, Java, Python 또는 C#과 같은 다양한 언어들로 스택을 구현할 수 있지만, 성능은 거의 동일하다.
스택의 기본적인 명령어
- Push : 스택의 최상단에 원소 추가
- Pop : 스택의 최상단에 위치한 원소 제거
- IsEmpty : 스택이 비어있는지 체크
- IsFull : 스택이 가득 찼는지 확인
- Peek : 스택의 최상단에 위치한 원소 값(value)를 읽어옴(제거하지 않는다)
스택의 동작방식
스택은 다음과 같은 방식으로 진행된다.
1. TOP 이라는 포인터를 생성해 스택의 최상단에 위치한 원소를 가르키도록 한다.
2. 스택이 초기화(Initializing)되었을 때, TOP 의 value 를 -1로 설정해 스택이 비었을 때 TOP == -1 을 사용하여 체크할 수 있도록 한다.
3. 원소를 push 할때마다, TOP 의 vaule를 증가시키고, TOP이 가르키는 위치에 새로운 원소를 추가한다.
4. 원소를 pop 할때마다, TOP 이 가르키는 위치의 원소를 return 하고, TOP 의 value 를 감소시킨다.
5. push 를 하기 전, 스택이 가득찼는지 체크한다.
6. pop 을 하기 전, 스택이 비어있는지 체크한다.

스택 구현
# Python
# stack 생성
def create_stack():
stack = []
return stack
# 비어있는 stack 생성
def check_empty(stack):
return len(stack) == 0
# stack에 원소 추가 (push)
def push(stack, item):
stack.append(item)
print("pushed item: " + item)
# stack의 원소 제거 (pop)
def pop(stack):
if (check_empty(stack)):
return "stack is empty"
return stack.pop()
stack = create_stack()
push(stack, str(1))
push(stack, str(2))
push(stack, str(3))
push(stack, str(4))
print("popped item: " + pop(stack))
print("stack after popping an element: " + str(stack))// Java
class Stack {
private int arr[];
private int top;
private int capacity; //stack의 size(용량)
// stack 생성
Stack(int size) {
arr = new int[size];
capacity = size;
top = -1;
}
// stack에 원소 추가 (push)
public void push(int x) {
//제일 먼저 stack이 가득찼는지 체크!
if (isFull()) {
System.out.println("OverFlow\nProgram Terminated\n");
System.exit(1);
}
System.out.println("Inserting " + x);
arr[++top] = x;
}
// stack의 원소 제거 (pop)
public int pop() {
// 항상 stack이 비어있는지 체크
if (isEmpty()) {
System.out.println("STACK EMPTY");
System.exit(1);
}
// pointer "top" 의 값을 감소시키는거라 실제 바로바로 원소를 날려버리는건 아니다.
return arr[top--];
}
// stack의 size를 return 하는 Utility function
public int size() {
return top + 1;
}
// stack이 비었는지 체크하는 function
public Boolean isEmpty() {
//스택이 비어있다면 top의 value는 -1이다.
return top == -1;
}
// stack이 가득찼는지 체크하는 function
public Boolean isFull() {
// stack이 가득찼다면, top의 value는 size - 1 이다. 즉 포인터가 최대치 부분을 가르키고 있다는것.
return top == capacity - 1;
}
public void printStack() {
for (int i = 0; i <= top; i++) {
System.out.println(arr[i]);
}
}
public static void main(String[] args) {
Stack stack = new Stack(5);
stack.push(1);
stack.push(2);
stack.push(3);
stack.push(4);
stack.pop();
System.out.println("\nAfter popping out");
stack.printStack();
}
}스택의 시간복잡도
array 기반의 push 와 pop 을 사용하는 stack은 O(1) 의 시간복잡도를 가진다.
스택을 사용해보자
스택은 구현하는데 있어 굉장히 간단하지만, 굉장히 효율적이다. 스택의 일반적인 용도는 다음과 같다.
- 문자열 뒤집기 : 후입선출(LIFO : Last In First Out)때문에 문자열을 스택에 넣고 (push) 다시 빼면 (pop) 문자열이 역순으로 나오게된다.
- 컴파일러 내부 연산 : 컴파일러는 스택을 사용하여 2 + 4 / 5 * (7 - 9 ) 와 같은 식을 전위 또는 후위연산(prefix or postfix)식으로 변환하여 계산한다.
- 브라우저 URL 체크 : 브라우저의 뒤로가기 버튼 또는 앞으로 가기 버튼을 누를 때 마다, 스택의 TOP(pointer) value가 감소 또는 증가하며 저장되어있는 URL로 이동한다. 새로운 페이지를 방문할 때 마다, 현재 URL이 스택의 최상단에 추가된다(push) 그리고 뒤로가기 버튼을 누르면 현재 URL이 스택에서 제거(pop)되고, 이전 URL로 이동하게된다.
'ETC > 자료구조 이론' 카테고리의 다른 글
| [JAVA] 다이나믹 프로그래밍 (Dynamic Programming) (0) | 2022.09.19 |
|---|---|
| [자료구조] Queue(큐) - Java, Python (0) | 2021.08.16 |
| [JAVA] 순차탐색(Sequential Search), 이진탐색(Binary Search) (0) | 2020.09.08 |


댓글