반응형
import itertoolsitertools 라이브러리를 사용하여 원소들의 순열과 조합을 사용할 수 있다.
1. 순열
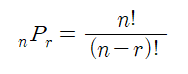
순열은 서로 다른 n개 중, r개를 나열하는 경우의 수로 permutations 함수를 사용한다.
def permutation(self):
# n=5, r=2
resultList = list(itertools.permutations(["1", "2", "3", "4", "5"], 2))
print("경우의 수 : {}개".format(len(resultList)))
print(*resultList, sep="\n")#결과
경우의 수 : 20개
('1', '2')
('1', '3')
('1', '4')
('1', '5')
('2', '1')
('2', '3')
('2', '4')
('2', '5')
('3', '1')
('3', '2')
('3', '4')
('3', '5')
('4', '1')
('4', '2')
('4', '3')
('4', '5')
('5', '1')
('5', '2')
('5', '3')
('5', '4')2. 중복순열
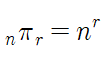
중복순열은 중복 가능한 n개 중, r개를 나열하는 경우의 수(순서있음) 로 product 함수에 repeat인자를 통해 계산한다.
def product(self):
# n=5, r=2
resultList = list(itertools.product(["1", "2", "3", "4", "5"], repeat=2))
print("경우의 수 : {}개".format(len(resultList)))
print(*resultList, sep="\n")#결과
경우의 수 : 25개
('1', '1')
('1', '2')
('1', '3')
('1', '4')
('1', '5')
('2', '1')
('2', '2')
('2', '3')
('2', '4')
('2', '5')
('3', '1')
('3', '2')
('3', '3')
('3', '4')
('3', '5')
('4', '1')
('4', '2')
('4', '3')
('4', '4')
('4', '5')
('5', '1')
('5', '2')
('5', '3')
('5', '4')
('5', '5')3. 조합
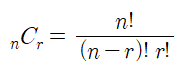
조합은 서로 다른 n개 중, r개를 선택하는 경우의 수(순서없음)로 combinations 함수를 사용한다.
def combinations(self):
# n=5, r=2
resultList = list(itertools.combinations(["1", "2", "3", "4", "5"], 2))
print("경우의 수 : {}개".format(len(resultList)))
print(*resultList, sep="\n")#결과
경우의 수 : 10개
('1', '2')
('1', '3')
('1', '4')
('1', '5')
('2', '3')
('2', '4')
('2', '5')
('3', '4')
('3', '5')
('4', '5')4. 중복조합
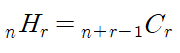
중복조합은 중복 가능한 n개 중, r개를 선택하는 경우의 수(순서없음)로 combinations_with_replacement 함수를 사용한다.
def combinations_with_replacement(self):
# n=5, r=2
resultList = list(itertools.combinations_with_replacement(["1", "2", "3", "4", "5"], 2))
print("경우의 수 : {}개".format(len(resultList)))
print(*resultList, sep="\n")#결과
경우의 수 : 15개
('1', '1')
('1', '2')
('1', '3')
('1', '4')
('1', '5')
('2', '2')
('2', '3')
('2', '4')
('2', '5')
('3', '3')
('3', '4')
('3', '5')
('4', '4')
('4', '5')
('5', '5')5. 리스트들 내 모든 원소들의 조합
2개 이상의 리스트(데이터셋)에서 모든 경우의 수를 뽑는 방법 역시 위에서 이야기했던것처럼 product 함수를 사용한다.
각 리스트를 개별적으로 넣어도 괜찮지만, 리스트가 많을 경우를 생각하여 * args 인자를 넣어 아래와 같이 표현한다.
def product_with_others(self):
firstList = ["A", "B", "C"]
secondList = [100, 200, 300]
thirdList = [0.001, 0.002, 0.003]
resultList = list(itertools.product(*[firstList, secondList, thirdList]))
print("경우의 수 : {}개".format(len(resultList)))
print(*resultList, sep="\n")#결과
경우의 수 : 27개
('A', 100, 0.001)
('A', 100, 0.002)
('A', 100, 0.003)
('A', 200, 0.001)
('A', 200, 0.002)
('A', 200, 0.003)
('A', 300, 0.001)
('A', 300, 0.002)
('A', 300, 0.003)
('B', 100, 0.001)
('B', 100, 0.002)
('B', 100, 0.003)
('B', 200, 0.001)
('B', 200, 0.002)
('B', 200, 0.003)
('B', 300, 0.001)
('B', 300, 0.002)
('B', 300, 0.003)
('C', 100, 0.001)
('C', 100, 0.002)
('C', 100, 0.003)
('C', 200, 0.001)
('C', 200, 0.002)
('C', 200, 0.003)
('C', 300, 0.001)
('C', 300, 0.002)
('C', 300, 0.003)
반응형
'ETC > 알고리즘 이론' 카테고리의 다른 글
| [알고리즘] 그리디 알고리즘 ( 탐욕 알고리즘 ) (Python, Java) (0) | 2021.10.19 |
|---|---|
| [알고리즘] 리스트의 모든 조합 구할때 고려할점 (permutations, combinations VS product) (Python) (0) | 2021.08.20 |
| [알고리즘] 재귀함수 (Recursive Function) (0) | 2021.08.02 |
| [알고리즘] 피보나치 수열(Fibonacci Sequence) 알고리즘 (JAVA) (0) | 2020.10.16 |
| [알고리즘] Towers of Hanoi - 하노이의 탑 알고리즘 (0) | 2020.10.04 |


댓글